Qbi's Weblog

Falls ihr euch schon immer mal gefragt habt, wie man ein reguläres 17-Eck mit Zirkel und Lineal konstruiert. Hier ist die Lösung:

Ich hatte meine Vortragsunterlagen zu einem Seminarvortrag kürzlich verbloggt. Mittlerweile ist auch die dazugehörige Ausarbeitung fertig. Die 257 kB große PDF-Datei behandelt den AES-Algorithmus und Public-Key-Verfahren (RSA und Diffie-Hellman-Schlüsseltausch). Vielleicht ist es für den einen oder anderen von Nutzen.

Das Clay Mathematics Institute ist bekannt für die Förderung der so genannten Milleniumsprobleme. Der Gewinner erhält eine Million US-Dollar ausgezahlt. Ein erster Aspirant für den Preis ist der Mathematiker Perelman, der 2002 die Poincaré-Vermutung bewiesen hat.

Seit kurzem stehen alle Bücher, die von dem Institut publiziert/finanziert worden sind, zum kostenlosen Download zur Verfügung. Falls ihr euch für analytische Zahlentheorie, Ricciflüsse oder ähnliches interessiert, besucht einfach die Online-Bibliothek.

Heute erhielt ich das Buch Algebra von Serge Lang. Das Buch ist in englischer Sprache und beim Durchblättern fiel mir auf, dass da was deutsches steht: Hilberts Nullstellensatz. Eigentlich hätte ich erwartet, dass sowas auch ins Englische gebracht wird. Aber es gab mal eine Zeit, in der Deutschland die führende Mathenation war. Wahrscheinlich hat sich der Name daher ins Englische gerettet.

Die Aussage des Satzes im obigen Buch ist: Let a be an ideal in k[X]. Let f be a polynomial in k[X] such that f(c)=0 for every zero (c)=(c₁, ..., c_n) of a in k^a. Then there exists an integer m>0 such that f^m in a. (Das “in” ist im Original ein Element-Zeichen.) Mikael hat in seinem Blog kürzlich eine äquivalente Formulierung vorgestellt.

Gestern hatte ich eine Klausur in Algebra. Diese lief recht gut. Jedoch gab es eine Aufgabe, für die ich absolut keine Idee hatte. Ich habe daran recht lange überlegt und, wie ich hinterher feststellte, gingen meine Gedanken in eine komplett falsche Richtung.

Im Grunde wollten die Prüfer die Anzahl der primitiven 2008-ten Einheitswurzeln wissen. Diese lässt sich mittels der Eulerschen φ-Funktion einfach berechnen:

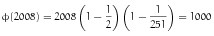
So verschenkt man mal eben zwei Punkte. Aber wenn meine Berechnungen stimmen, habe ich 25 von 23 Punkten. Also sehe ich da mal großzügig über den Lapsus hinweg.

Das neue Semester hat begonnen. Diverse Zitate aus der ersten Woche zeugten bereits davon. Ich habe mich für vier Vorlesungen in diesem Semester entschieden:

Algebra I

Nichtmathematiker meinen hier immer, dass sei ja eine Erstsemestervorlesung und fragen sich/mich, warum ich die denn jetzt erst höre. Sie verwechseln das mit linearer Algebra (und analytischer Geometrie), die man in der Tat im ersten Semester hört. In Algebra geht es im wesentlichen um die Galoistheorie , d.h. um die Lösung von Polynomen. Ich halte es für wichtig, die Vorlesung zu besuchen, da hier Grundlagen für weitere Algebrafächer gelegt werden und später das Verständnis sicher erleichtern. Momentan halten wir uns bei der Gruppentheorie auf. Das wurde bereits in den Vorlesungen zu linearer Algebra recht vertiefend erklärt, so dass das eher Wiederholung ist.

Algorithmik

Algorithmik ist die zweite Basisvorlesung. Sie stammt aus dem Bereich der theoretischen Informatik und behandelt den Entwurf und Analyse von Algorithmen.

Brownsche Bewegung

Die Brownsche Bewegung (auch Wiener Prozess genannt) kennt wahrscheinlich jeder. Man legt kleine Teilchen in eine Flüssigkeit und diese tanzen dann wild umher. Albert Einstein hat dann später ein mathematisches Modell für diese Bewegung entwickelt. Das Integral sieht wirklich furchterregend aus. Heutzutage wird die Brownsche Bewegung für die Theorie von zufälligen Prozessen verwendet.

Darstellungstheorie

Dies ist wieder eine algebraische Vorlesung. Der Artikel in der Wikipedia schreibt: Die Grundidee ist, die Elemente einer Gruppe durch Transformationen bestimmter mathematischer Gegenstände darzustellen. Die mathematischen Gegenstände sind in dem Fall Matrizen. Eine Besonderheit der Vorlesung ist, dass sie in englisch gehalten wird. Das verursachte bei mir unerwarteteterweise anfangs Probleme. Denn ich bin es nicht gewohnt, englisch zu schreiben und zu denken. Da der Professor auch ziemlich schnell schreibt, kam ich zuerst nicht mit. Bis ich auf die Idee kam, die Vorlesung simultan zu übersetzen und auf deutsch mitzuschreiben. Damit kam ich dann wieder mit Mitschreiben und -denken mit.

In der Vorlesung Algebra I wurden heute elementare Begriffe, wie Halbgruppe, Gruppe, Homomorphismus etc. eingeführt. Zu Beginn meinte der Vorlesende:

Bewerfen Sie mich mit Papierbällchen, wenn Ihnen das zu trivial ist.