Bislang konnte ich die Eulerschen Probleme mit einem naiven Programmieransatz lösen. Das heißt, die erste Idee, die mir in den Kopf kam, schrieb ich runter und bekam eine Lösung. Das zehnte Problem warf mir einen Stock zwischen die Beine. Erstmals musste ich mir Gedanken über die Optimierung des Codes machen.
Das zehnte Problem klingt erstmal ganz harmlos: Finden Sie die Summen aller Primzahlen, die kleiner als 2 000 000 sind.. Ha, das ist ja eine einfache Fingerübung:
sieb = [ i for i in xrange(2,2000000) ]
for i in xrange(2,2000000):
for j in xrange(2,2000000):
if i*j in sieb:
sieb.remove(i*j)
Die Werte in sieb müssen dann nur noch addiert werden und fertig. Jedoch kam ich gar nicht soweit. Denn das Programm lief und lief und lief.
Das brachte mich zum Nachdenken, woran das liegen könnte. Letztlich ist die Ursache offensichtlich. Denn der Code berechnet jedes Produkt. Dafür werden schon 2 000 000 * 2 000 000 = 4 000 000 000 000 Berechnungen durchgeführt. Wenn man von der (viel zu optimistischen) Variante ausgeht, dass jede Berechnung ein CPU-Zyklus ist, würde das Programm auf aktuellen Architekturen länger als eine halbe Stunde laufen. In der Realität lief es 15 Stunden. Wie lässt sich die Laufzeit nun verbessern?
Es ist recht offensichtlich, dass das Programm zuviel berechnet. Im ersten Schleifendurchlauf gibt es die Multiplikationen: 2*2, 2*3, 2*4, ..., 2*1999999 = 3999998. Beim zweiten Schleifendurchlauf: 3*2, 3*3, 3*4, ..., 3*1999999 = 5999997. Am klarsten fällt es im letzten Durchlauf auf: 1999999*2, 1999999*3, ..., 1999999*1999999 = 3999996000001. Die Berechnung 3*2 wurde schon im ersten Schritt (nur umgekehrt mit 2*3) durchgeführt. Hier wirkt das Kommutativgesetz. Also kann die Schleife im zweiten Durchlauf erst bei drei beginnen. Im dritten Durchlauf würde nach obigem Algorithmus 4*2, 4*3, 4*4 usw. berechnet werden. Verallgemeinert lässt sich also sagen, dass die Variable der zweiten Schleife genausogroß oder größer als die erste Variable sein muss. Dieser Schritt halbiert die Zahl der Berechnungen.
In der obigen Darstellung wird klar ersichtlich, dass das Programm nicht in jedem Fall bis zum Maximum von 2 000 000 laufen muss. Schon im ersten Durchlauf werden Werte über 2 000 000 berechnet. Das heißt, das Produkt i*j muss kleiner oder gleich 2 000 000 sein. Umformen nach j ergibt: j?2 000 000/i. Eine weitere oft genutzte Optimierung ist es, die erste Schleifenvariable nur bis ?2000000 laufen zu lassen.
Weiterhin fiel mir auch ein, dass man schon die initiale Liste nicht mit Zahlen von 2 bis 2 000 000 füllen muss. Denn es ist bekannt, dass alle Vielfachen von 2 sofort ausfallen. Man kann sogar soweit gehen, dass man nur Zahlen nach dem Muster 6*n-1 und 6*n+1 aufnimmt. Denn die Zahlen 6*n+0, 6*n+2 und 6*n+4 sind gerade und damit keine Primzahlen. Die Zahl 6*n+3 entspricht 3(2*n+1) und ist somit durch drei teilbar. Es verbleibt das obige Muster.
Theoretisch hätetn die obigen Anpassungen schon reichen sollen, um die Laufzeit unter eine Minute zu drücken. Jedoch lief das Programm immer nach weitaus länger. Nach einigem Stöbern fiel mir dann auf, dass in Python die Listenoperationen in und remove die Listen von Beginn an durchsuchen. Das bringt natürlich nochmal eine extreme Pessimierung der Laufzeit. Stattdessen sollte man hier Sets oder Dictionaries nutzen. Ich habe es mit Sets probiert und prompt lief das Programm schnell genug.
sieb = {}
for i in xrange(2, 2000000):
sieb[i] = True
for x in xrange(2,int(math.sqrt(2000000))+1):
if sieb[x] == True:
for y in xrange(2000000/x, x-1,-1):
t = x * y
sieb[t] = False
Grundsätzlich lassen sich weitere Möglichkeiten der Optimierung ausdenken. Jedoch reichte mir das obige Ergebnis, um das Ziel zu erreichen. Wahrscheinlich benötige ich in späteren Aufgabe noch eine weitere Verbesserung.


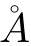 Der Kringel rutscht halb vom A runter. Insgesamt sieht das merkwürdig aus. Das weitere Dokument hat keine weiteren Hinweise. Also versuche ich es mit
Der Kringel rutscht halb vom A runter. Insgesamt sieht das merkwürdig aus. Das weitere Dokument hat keine weiteren Hinweise. Also versuche ich es mit 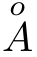 . Auch hier steht der Kringel deutlich zu weit links. Außerdem ist die gesamte Kombination zu groß. Insbesondere bei Überschriften ragt der Kringel schon in den Überschriftentext hinein. Nach ein wenig weiterer Suche stiess ich dann auf das Paket accents. Mit der Anweisung
. Auch hier steht der Kringel deutlich zu weit links. Außerdem ist die gesamte Kombination zu groß. Insbesondere bei Überschriften ragt der Kringel schon in den Überschriftentext hinein. Nach ein wenig weiterer Suche stiess ich dann auf das Paket accents. Mit der Anweisung 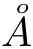 . Das sieht, wie ich finde, perfekt aus.
. Das sieht, wie ich finde, perfekt aus.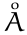 .
.